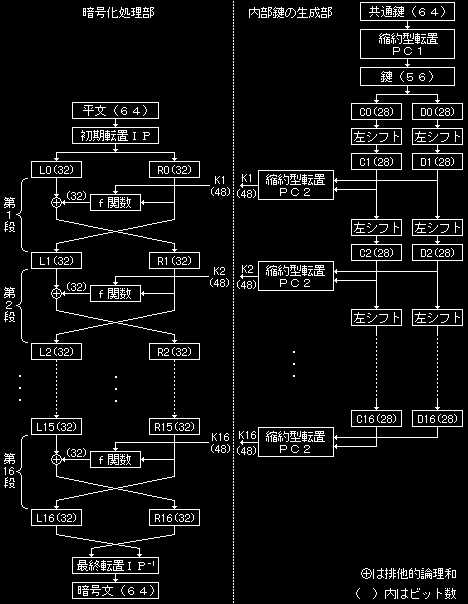
図1.DESの構成
1.DES
DESはデータ暗号化規格(Data Encryption Standard:DES)の略称で、米国商務省標準局(NBS)の暗号アルゴリズムの公募した中から候補にあがった、1974年にIBMで開発されたルシファー
(Lucifer)をもとにできあがったものです。1977年にDESという名で公布され、1981年には米国規格協会(ANSI)も、DESをDEA(Data
Encryption Algorihm)という名称で標準化しました。
DESは1ブロック64ビットとして扱い、鍵は7バイトの鍵データと1バイトの奇数パリティから成り立っています。そして、暗号の鍵は暗号の制作者と受信者が共有する方式です。
当時のDESには並列処理を行う専用ハードウェアを必要とし、製造も許可により限られていたため、その安全性の評価もできなったのですが、コンピュータの発達した現在では、ソフトウェアだけで使用できるポピュラーな暗号になっています。UNIXのログイン時のユーザ認証や電子メール、ネットワーク機器など幅広く使用されていますので、目にする機会もあるでしょう。
当時の暗号技術の総決算であったDESには、開発から10年以上も後に考案され発表された、差分暗号攻撃法(1990)に対する対策がすでに考慮されていました。
あらゆる攻撃法も考慮しながら、アルゴリズムを組み立てていったということなのでしょうね。
いやはや、素晴らしいというべきか、すきがないというべきか。
2.DESの暗号化アルゴリズム
それでは、本題であるDESの暗号化アルゴリズムを見てみましょう。
DESによる暗号化をブロック図で表すと、図1のようになります。

う〜ん、思っていたより複雑じゃないですね〜。これだけ見ると共通鍵なしで暗号文から平文へ逆算できそうな気がするのですが、16段ある排他的論理和が邪魔してくれています。
・排他的論理和(ExOR)
わからない人もいますので説明します。
排他的論理和とはふたつの値が一致したときに0、一致しないときに1になる論理演算です。それが各ビットで行われます。
表で表すと次のようです。
a b | (a ExOR b) ---------+------------ 0 0 | 0 0 1 | 1 1 0 | 1 1 1 | 0
一見すると、これじゃあ復元もできないじゃないかと思われるかも知れませんが、実は入力した片方ともう一度排他的論理和を行うと、残りの入力した片方が出力されるという特性があります。
つまり、(a ExOR b)からaを取り出すには、bと排他的論理和を行えばよいのです。
a = (a ExOR b) ExOR b
面白い特性ですね。でも、bがわからないことにはaもわからないという、一般の演算とかわりありませんけどね。
では、DES暗号化アルゴリズムを各部分ごとに詳細な説明していくことにします。
(1)暗号化処理部
まずは暗号化処理部の方についての説明です。
暗号化は平文を64ビット(=8文字)ずつに区切って、それぞれを64ビットの暗号文に暗号化していきます。ただし日本語など全角文字を処理する場合には、1文字に16ビット必要なため、一度に4文字ずつ暗号化していくことになります。
<処理の流れ>
DESは図1からもわかるように、64ビットの平文を入力して初期転置を行っています。次にこの64ビットを左右32ビットずつにわけ、L(32)とR(32)になります。そして、R(32)はf関数に入力され、f関数は32ビットを返してきます。このf関数に関しては、また後で説明します。f関数の出力とL(32)で排他的論理和をとったものが次段のR(32)となり、R(32)はそのまま次段の
L(32)へ移ります。
この動作を16段行い、最後に最終転置を経て、やっと暗号文になります。
これがおおざっぱなDESのアルゴリズムです。
それでは、ブロック図で使われている初期転置、最終転置について説明します。
・初期転置IPのボックスを通過する場合、次のような転置処理を行います。
| 1 2 3 4 5 6 7 8 ----+---------------------------------------- 0 | 58 50 42 34 26 18 10 2 8 | 60 52 44 36 28 20 12 4 16 | 62 54 46 38 30 22 14 6 =L(32) 24 | 64 56 48 40 32 24 16 8 | 32 | 57 49 41 33 25 17 9 1 40 | 59 51 43 35 27 19 11 3 48 | 61 53 45 37 29 21 13 5 =R(32) 56 | 63 55 47 39 31 23 15 7
この表は、左上が1ビット目で8ビットずつ並べています。
これは表の並びが出力側のビット番号で、表内の数字が入力側のビット番号に対応して転置されます。
これだけではわかりにくいので、この転置の例を上げてみましょう。
仮に、入力がa(64)で出力がb(64)としますと、次のようになります。
a[58] ---> b[1] a[50] ---> b[2] : a[15] ---> b[63] a[7] ---> b[64]
注意)ここでのa[n]は、aのnビット目という意味です。
入力は64ビットで、出力の0〜32ビットまでがL(32)、33〜64ビットまでがR(32)となります。
・最終転置IP−1のボックスを通過する場合、次のような転置処理を行います。
| 1 2 3 4 5 6 7 8 ----+---------------------------------------- 0 | 40 8 48 16 56 24 64 32 8 | 39 7 47 15 55 23 63 31 16 | 38 6 46 14 54 22 62 30 24 | 37 5 45 13 53 21 61 29 32 | 36 4 44 12 52 20 60 28 40 | 35 3 43 11 51 19 59 27 48 | 34 2 42 10 50 18 58 26 56 | 33 1 41 9 49 17 57 25
なお、この最終転置の入力ビット列は、上位32ビットがR16、下位32ビットがL16となる64
ビットです。
この出力が、64ビット(=8文字)の暗号文となります。
(2)内部鍵の生成部
次に、内部鍵の生成部について説明します。
入力される共通鍵は64ビット、うち奇数パリティビット8ビットなので実質的な鍵の長さは
56ビットです。ただし、パリティビットも存在するビット列として、64ビットで考えていきます。
また、この共通鍵さえわかれば暗号文の複合も可能なので、もっとも重要な部分といえます。
ちなみに、奇数パリティビットとは情報のまとまりごと(この場合7ビットごと)に1ビットの検査ビットを設けて、そのビットを含めて1であるビットの総数が常に奇数個になるようにするものです。共通鍵の8,16,24,32,40,48,54,64ビット目が、奇数パリティビットになります。
情報を伝達する際よく用いられる方法で、転送中に1ビットの誤りが発生してもエラーが検出できることになります。
<処理の流れ>
まず、64ビットの共通鍵を入力して縮約型転置1を行います。縮約型転置1では64ビットを
C(28)とD(28)にわけ、それぞれの道を歩ませます。次に、わけられたC(28)とD(28)は、それぞれ循環シフトとして一定のスケジュールに従った数だけ左シフトします。左シフトされたC(28)と
D(28)は、縮約型転置2を通してK(48)を作成してf関数に受け渡します。以下、左シフトされた
C(28)とD(28)をさらに一定のスケジュールに従った数だけ循環左シフトしていきます。
この動作を16段行って、各段に対応したK(48)を16個作成します。
内部鍵K1〜K16の誕生です。
それでは縮約型転置1、左シフトのスケジュール、縮約型転置2の説明をします。
・縮約型転置PC1のボックスを通過する場合、次のような転置処理を行います。
| 1 2 3 4 5 6 7 ----+----------------------------------- 0 | 57 49 41 33 25 17 9 7 | 1 58 50 42 34 26 18 14 | 10 2 59 51 43 35 27 =C(28) 21 | 19 11 3 60 52 44 36 | 28 | 63 55 47 39 31 23 15 35 | 7 62 54 46 38 30 22 42 | 14 6 61 53 45 37 29 =D(28) 49 | 21 13 5 28 20 12 4
表の並びは、初期転置で説明したとおりです。
入力は64ビットで、出力は0〜28ビットまでがC(28)となり、29〜56ビットまでがD(28)となります。
・左シフトのボックスを通過する場合、段数によって次のようなスケジュールに従って循環左シフトを行います。
段数 | 左シフトの数 ------+-------------- 1 | 1 2 | 1 3 | 2 4 | 2 5 | 2 6 | 2 7 | 2 8 | 2 9 | 1 10 | 2 11 | 2 12 | 2 13 | 2 14 | 2 15 | 2 16 | 1
だだし、このシフトは循環シフトなので注意が必要です。
たとえば、a(28)を循環シフトで1つ左シフトしたものをb(28)とした場合は、
a(28) = a[1],a[2],a[3],,a[26],a[27],a[28] b(28) = a[2},a[3],a[4],,a[27],a[28],a[1]
のようになります。つまり、各ビットが左に1ビットずれて、ビット列から追い出された最上位ビットが最下位ビットとして追加されます。
まさに言葉通り、循環することになりますね。
ちなみに計28シフトしていますので、C0(28)=C16(28),D0(28)=D16(28)と一巡することになります。
おそらく、暗号文を復元するときに処理を楽にするためなのでしょう。
・縮約型転置PC2のボックスを通過する場合、次のような転置処理を行います。
| 1 2 3 4 5 6 ----+------------------------------ 0 | 14 17 11 24 1 5 6 | 3 28 15 6 21 10 12 | 23 19 12 4 26 8 18 | 16 7 27 20 13 2 24 | 41 52 31 37 47 55 30 | 30 40 51 45 33 48 36 | 44 49 39 56 34 53 42 | 46 42 50 36 29 32
なお、このボックスへの入力ビット列は、上位28ビットがC(28)、下位28ビットがD(28)の56ビットとなります。
出力は48ビットのK(48)となり、f関数に渡されます。
(3)f関数
では、最後のブラックボックスとなったf関数について説明します。
f関数は図2のような構成をしています。
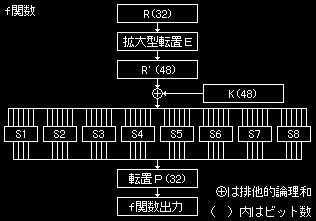
<処理の流れ>
まず、暗号化処理部より入力されてきたR(32)は、拡大型転置により48ビットになります。そして、内部鍵の生成部から入力されてきたK(48)と排他的論理和を行います。次に、その結果の48ビットを上位6ビットから8つにわけて各Sボックスを通し、4ビットとして吐き出させます。この4ビットを
32ビットの並びとして集め、転置を行ったものをf関数の出力とします。
それでは、拡大型転置とSボックス、転置Pについて説明します。
・拡大型転置Eのボックスを通過する場合、次のような転置処理を行います。
| 1 2 3 4 5 6 ----+------------------------------ 0 | 32 1 2 3 4 5 =S1(6) 6 | 4 5 6 7 8 9 =S2(6) 12 | 8 9 10 11 12 13 =S3(6) 18 | 12 13 14 15 16 17 =S4(6) 24 | 16 17 18 19 20 21 =S5(6) 30 | 20 21 22 23 24 25 =S6(6) 36 | 24 25 26 27 28 29 =S7(6) 42 | 28 29 30 31 32 1 =S8(6)
入力32ビットに対して、48ビットで出力します。
続いて6ビットずつに区切り、表で示すように各Sボックスへ渡します。
・各Sボックスを通過する場合、次のような処理を行います。
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -------+---------------------------------------------------------------- S1 00 | 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7 01 | O 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8 10 | 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0 11 | 15 12 8 2 4 9 1 7 5 11 3 14 10 O 6 13 -------+---------------------------------------------------------------- S2 00 | 15 1 8 14 6 11 3 4 9 7 2 13 12 O 5 10 01 | 3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5 10 | 0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15 11 | 13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9 -------+---------------------------------------------------------------- S3 00 | 10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8 01 | 13 7 O 9 3 4 6 10 2 8 5 14 12 11 15 1 10 | 13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7 11 | 1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12 -------+---------------------------------------------------------------- S4 00 | 7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15 01 | 13 8 11 5 6 15 O 3 4 7 2 12 1 10 14 9 10 | 10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4 11 | 3 15 O 6 10 1 13 8 9 4 5 11 12 7 2 14 -------+---------------------------------------------------------------- S5 00 | 2 12 4 1 7 10 11 6 8 5 3 15 13 O 14 9 01 | 14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6 10 | 4 2 1 11 10 13 7 8 15 9 12 5 6 3 O 14 11 | 11 8 12 7 1 14 2 13 6 15 O 9 10 4 5 3 -------+---------------------------------------------------------------- S6 00 | 12 1 10 15 9 2 6 8 O 13 3 4 14 7 5 11 01 | 10 15 4 2 7 12 9 5 6 1 13 14 O 11 3 8 10 | 9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6 11 | 4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13 -------+---------------------------------------------------------------- S7 00 | 4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1 01 | 13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6 10 | 1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2 11 | 6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12 -------+---------------------------------------------------------------- S8 00 | 13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7 01 | 1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2 10 | 7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8 11 | 2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11
ここでは、入力6ビットに対して、4ビットで出力します。
今までの表とは少し違うので、具体例を挙げて説明しましょう。
仮に、S1に011001の6ビットが入力データとして入ったとします。ここではまず、最上位と最下位ビットの2ビットを取り出します。この場合、2進数01となります。ついで最上位と最下位ビットが取り除かれた4ビットを、10進数に変換します。この場合2進数
1100ですから、10進数では12となります。入力されたのはS1ですから、S1テーブルの01行の12列を見ますと10進数で9が得られます。これを2進数に変換した1001という4ビットが、出力されることになります。
ちょっとややこしい計算ですね。
しかも、各Sボックスごとでテーブルが違いますので、注意が必要です。
・転置Pのボックスを通過する場合、次のような転置処理を行います。
| 1 2 3 4 ----+-------------------- 0 | 16 7 20 21 4 | 29 12 28 17 8 | 1 15 23 26 12 | 5 18 31 10 16 | 2 8 24 14 20 | 32 27 3 9 24 | 19 13 30 6 28 | 22 11 4 25
入力される32ビットの並びは、上位4ビットごとにS1、S2と並べられたものです。
出力も32ビットで、この後、暗号化処理部でL(32)と排他的論理和が行われる運命とあいなります。
(4)DESの暗号化の実行例
実行例をそのまま書き出すと、0,1の羅列が続きますのでこちらの方で示します。
実行例
なお、実行例はここに記述した通りの暗号化アルゴリズムに従っています。実際のDES暗号でこの通りの結果になるかは未確認ですので、ご了承ください。
3.まとめ
現在、DES暗号化のアルゴリズムはこのように公開されています。そのため、共通鍵さえわかれば暗号文を平文として複合することができます。
しかし、この共通鍵の割り出しに「総当たり攻撃」という鍵をしらみつぶしに試す方法を行うとすると、この56ビットの鍵から生成できる内部鍵の組み合わせは2の56乗という膨大な数を必要とします。(2の56乗
≒ 7.2×1016)
この共通鍵を求めるためには現在でも多くの演算時間を必要としますが、100万ドル程度で専用の解読機を製作すれば、数時間で暗号化の鍵を見つけることができるといわれていました。
しかし、100万ドルもかけなくても、1998年1月13日に米国RSA DATA Security社から主催された第1回暗号解読コンテストによって解読されました。これは22,000人の参加者により、5万台以上の一般パソコンを導入して、わずか39日で解読されたのです。
そして、その半年後の1998年7月13日に開催された第2回暗号解読コンテストでは、制作費25万ドルのEFFの専用ハードウェアによって、2日と8時間で解読されたのです。
このように短い時間で解読されてしまい、すたれゆくDESのように感じられますが、実は「DESは群を成さない」という論理を利用して暗号を強化することができます。たとえば3重に暗号化する方法(triple-DES)などがあり、DES生き残りのための一つの方策となっています。
しかし、これらDES暗号よりも、高い評価を受けているものはいくつかあります。それらがそのままスタンダードへとならないのは、暗号攻撃方法が次々と登場する中で歴史が浅いこと、また、DESとの互換性の確保と従来のDESへの投資などがあり、おいそれと鞍替えというわけにはいかないのが現状のようです。
近い将来、DESは消え去るでしょう。しかし、DESの公開された暗号化技術は、その後の誕生した暗号化方法の基礎として、参考されたことは間違いありません。私たちがこの技術を学ぶということは、新しく誕生した暗号化方法を学ぶことになるのかも知れません。
以上、長く堅苦しい文につき合ってくれましたことを感謝いたします。
〜〜 お わ り 〜〜
参考文献 [1]吹田智章:暗号の全てがわかる本, 技術評論社出版, 1998 [2]Federal Information Processing Standards Publication 46-2 - (DES), 1993 December 30 http://www.nist.gov/itl/div897/pubs/fip46-2.htm [3]Security for computer networks http://www.etl.go.jp/etl/bunsan/‾thiguchi/Security [4]Kikuchi Masaki's Home Page, 暗号と情報セキュリティ(暗号班) http://mercury.ecs.cst.nihon-u.ac.jp/‾masaki/kenkyu/security.html [5]日新電機株式会社 セキュリティ営業部, ELNIS home page 1998 進化するネットワークセキュリティ 全7回 http://www.elnis.com/MISC/angou.html [6]RSA Data Security, Inc. RSA FAQ World http://www.rsa-japan.co.jp/faq/index.html [7]Kenji Rikitake's Cyberscope Lite: 18-JUL-1998 http://www.k2r.org/kenji/jp-cyberscope/jp-cyberscope-lite-19980718.html